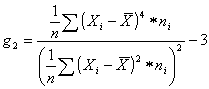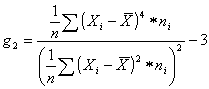Principales características de la disperción
Principales características de la disperción
Estadística
Jorge F. Jorge R. | 23 feb 2020
El objetivo del estudio de los parámetros estadísticos es obtener información resumida del conjunto de datos en los que estamos interesados. Ya hemos resumido nuestros datos en un número, por ejemplo la media. Pero ¿es representativo ese valor?
Comencemos con un ejemplo.
"Supongamos que dos alumnos han realizado cinco exámenes cada uno. Para evaluarlos elegimos hacer la media de las cinco notas que han obtenido.
Las notas han sido:
ALUMNO 1: 4, 5, 5, 5, 6. Media = 5
ALUMNO 2: 1, 2, 5, 8, 9. Media = 5
Si vemos los dos tendrían la misma nota, lo que nos haría pensar que los dos alumnos son similares, pero si observamos sus notas hay una gran diferencia entre ambos. El alumno 1 tiene unas notas muy homogéneas, muy próximas a la media mientras que el segundo tiene unos resultados muy dispares."
Para poder analizar bien sus resultados necesitaríamos otro parámetro que nos mida esa variabilidad. Estamos hablando de las medidas de dispersión.
Las medidas de dispersión son parámetros estadísticos que nos informan sobre la variabilidad de los datos, es decir, si la distribución de los datos es más o menos homogénea y por tanto nos dan una medida sobre la representatividad de los parámetros de centralización (moda, mediana o media)
Comencemos con un ejemplo.
"Supongamos que dos alumnos han realizado cinco exámenes cada uno. Para evaluarlos elegimos hacer la media de las cinco notas que han obtenido.
Las notas han sido:
ALUMNO 1: 4, 5, 5, 5, 6. Media = 5
ALUMNO 2: 1, 2, 5, 8, 9. Media = 5
Si vemos los dos tendrían la misma nota, lo que nos haría pensar que los dos alumnos son similares, pero si observamos sus notas hay una gran diferencia entre ambos. El alumno 1 tiene unas notas muy homogéneas, muy próximas a la media mientras que el segundo tiene unos resultados muy dispares."
Para poder analizar bien sus resultados necesitaríamos otro parámetro que nos mida esa variabilidad. Estamos hablando de las medidas de dispersión.
Las medidas de dispersión son parámetros estadísticos que nos informan sobre la variabilidad de los datos, es decir, si la distribución de los datos es más o menos homogénea y por tanto nos dan una medida sobre la representatividad de los parámetros de centralización (moda, mediana o media)
En una distribución de datos, las medidas de dispersión tienen un papel muy importante. Estas medidas complementan a las de posición central, caracterizando la variabilidad de los datos. Así, las medidas de tendencia central indican valores con respecto a los que los datos parecen agruparse. Son recomendadas para inferir el comportamiento de variables en poblaciones y muestras. Algunos ejemplos de ellas son la media aritmética, la moda o la mediana.
Medidas de dispersión
Rango
En primer lugar, el rango está recomendado para una comparación primaria. De esta manera, considera solo las dos observaciones extremas. Por eso se recomienda solo para muestras pequeñas. Se define como la diferencia entre el último valor de la variable y el primero.
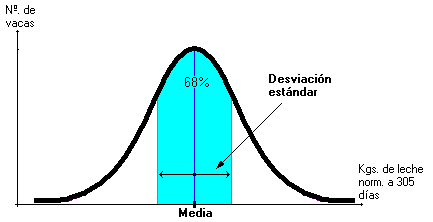
Desviación estadística
Por su parte, la desviación media indica dónde estarían concentrados los datos si todos estuvieran a la misma distancia de la media aritmética.
Varianza
La varianza es una función algebraica de todos los valores,
apropiada para tareas de estadística inferencial.
Se puede definir como las desviaciones al cuadrado.
Villasante P. (2019), MEDIDAS DE DISPERSIÓN EN ESTADÍSTICA: Lamenteesbrillante (8 julio, 2019), Recuperado: https://lamenteesmaravillosa.com/las-medidas-de-dispersion-en-estadistica/
Medidas de distribución
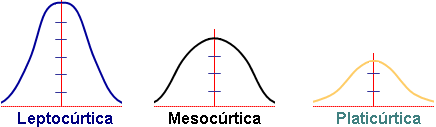
Curtosis
También conocida como medida de apuntamiento, es una medida estadística, que etermina el grado de concentración que presentan los valores en la región central de la distribución. Por medio del Coeficiente de Curtosis, podemos identificar si existe una gran concentración de valores (Leptocúrtica), una concentración normal (Mesocúrtica) ó una baja concentración (Platicúrtica)
Existen algunas variables que presentan un mayor grado de concentración (menor dispersión) de los valores en torno a su media y otras, por el contrario, presentan un menor grado de concentración (mayor dispersión) de sus valores en torno a su valor central. Por tanto, la curtosis nos informa de lo apuntada (mayor concentración) o lo achatada (menor concentración) que es una distribución.
Para calcular el coeficiente de Curtosis se utiliza la ecuación
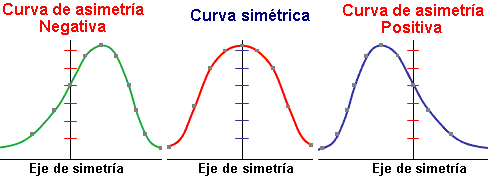
Asimetría
Nos permite identificar si los datos se distribuyen de forma uniforme alrededor del punto central (Media aritmética). La asimetría presenta tres estados diferentes, cada uno de los cuales define de forma concisa como están distribuidos los datos respecto al eje de asimetría. Se dice que la asimetría es positiva cuando la mayoría de los datos se encuentran por encima del valor de la media aritmética, la curva es Simétrica cuando se distribuyen aproximadamente la misma cantidad de valores en ambos lados de la media y se conoce como asimetría negativa cuando la mayor cantidad de datos se aglomeran en los valores menores que la media.
El Coeficiente de asimetría, se representa mediante la ecuación matemática
Martínez G. A. (2005), Medidas de distribución - Asimetría y Curtosis (2015): SPSS . Recuperado: http://www.spssfree.com/curso-de-spss/analisis-descriptivo/medidas-de-distribucion-curtosis-asimetria.html
El teorema del límite central: las medias de muestras grandes y aleatorias son aproximadamente normales
Es un teorema fundamental de probabilidad y estadística. Describe la distribución de la media de una muestra aleatoria proveniente de una población con varianza finita. Cuando el tamaño de la muestra es lo suficientemente grande, la distribución de las medias sigue aproximadamente una distribución normal.
El teorema se aplica independientemente de la forma de la distribución de la población. Muchos procedimientos estadísticos comúnes requieren que los datos sean aproximadamente normales. El teorema de límite central le permite aplicar estos procedimientos útiles a poblaciones que son considerablemente no normales. El tamaño que debe tener la muestra depende de la forma de la distribución original. Si la distribución de la población es simétrica, un tamaño de muestra de 5 podría producir una aproximación adecuada. Si la distribución de la población es considerablemente asimétrica, es necesario un tamaño de muestra más grande. Por ejemplo, la distribución de la media puede ser aproximadamente normal si el tamaño de la muestra es mayor que 50. Las siguientes gráficas muestran ejemplos de cómo la distribución afecta el tamaño de la muestra que se necesita.
Distribución uniforme Medias de las muestras
Página web consultada: https://support.minitab.com/es-mx/minitab/18/help-and-how-to/statistics/basic-statistics/supporting-topics/data-concepts/about-the-central-limit-theorem/
Temas relacionados:
Esta web se reserva el derecho de suprimir, por cualquier razón y sin previo aviso, cualquier contenido generado en los espacios de participación en caso de que los mensajes incluyan insultos, mensajes racistas, sexistas... Tampoco se permitirán los ataques personales ni los comentarios que insistan en boicotear la labor informativa de la web, ni todos aquellos mensajes no relacionados con la noticia que se esté comentando. De no respetarse estas mínimas normas de participación este medio se verá obligado a prescindir de este foro, lamentándolo sinceramente por todos cuantos intervienen y hacen en todo momento un uso absolutamente cívico y respetuoso de la libertad de expresión.
No hay opiniones. Sé el primero en escribir.
Te recomendamos...
