La derivada es una herramienta matemática para ello. Isaac Newton desarrolló los principios del cálculo diferencial en su obra Methodus Fluxiorum et Serierum Infinitorum (1671). En ese trabajo, da los pasos precisos alrededor de los conceptos de función y de límite, que le permiten plantear matemáticamente cuando las cantidades varían infinitesimalmente y, de esta forma, describir el movimiento de un punto que traza una curva, situación que expresa de la siguiente forma:

Por última proporción de cantidades evanescentes debemos entender el cociente de estas cantidades, no antes de que desvanezcan, ni después, pero tal como se van desvaneciendo. La parte infinitesimal pequeña en la que un fluente se incrementa por unidad de tiempo cero es el momento del fluente.

Análisis del planteamiento de Isaac Newton

El texto reseñado puede analizarse en dos partes; la primera habla de cantidades evanescentes, es decir que se desvanecen o tienden a ser infinitamente pequeñas. Esto se puede contrastar directamente de la definición de límite: “[...] se dice que ‘L’ es el límite de la función ‘f(x)’ cuando la variable ‘x’ tiende al valor ‘a’ si la diferencia entre ‘f(x)’ y ‘(L)’ puede hacerse tan pequeña como se desee…”. En un cociente de cantidades con estas características, completa el texto.

Mientras la segunda parte habla de una parte infinitesimalmente pequeña que incrementa las variables (el fluente indica la letra) por unidad de tiempo.

Una vez extraídos estos elementos, se deben regresar al contexto sobre el que Newton trabajaba (el movimiento de una partícula), lo cual se ilustra a continuación:

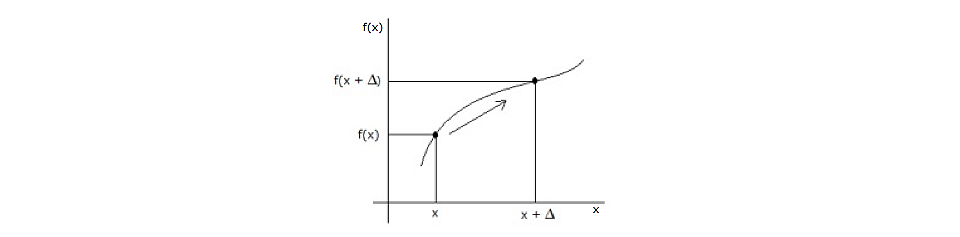
En este escenario se observa que, sobre la curva descrita por el movimiento, hay un par de puntos y una diferencia entre estas posiciones en una proporción de cantidades que se hace cada vez más pequeña (evanescentes tanto como se desee, según el concepto de límite) por unidad de tiempo; a partir de esta discusión, se puede plantear la ecuación que describe esa acción de movimiento:

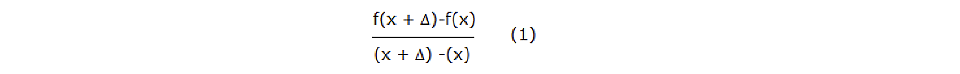
Al observar la ecuación (1), destaca la diferencia entre las posiciones (no en vano el término cálculo diferencial) con la parte infinitesimal en que se incrementa, numerador, tiempo (unidad de tiempo) y su correspondiente incremento en el denominador. El significado de la ecuación (1), según lo que ya conoces sobre el tema de funciones, es que ésta corresponde con la pendiente de la recta definida por los dos puntos del movimiento estudiado por Newton; de esta manera, se observa la formación de una recta secante (por definición, que corta a la curva en dos puntos) y se puede interpretar como se muestra a continuación:

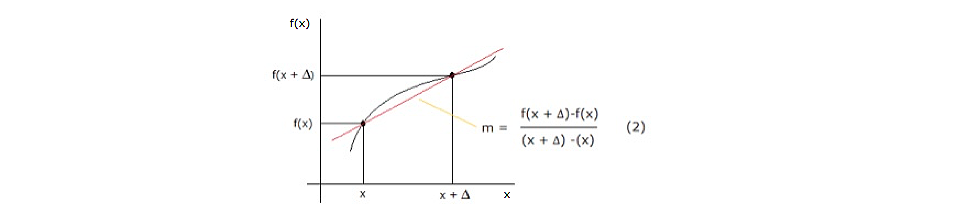
Adicionalmente a la interpretación matemática de pendiente, se tiene que en física esta misma relación define la velocidad promedio a que se mueve un objeto en la trayectoria planteada (cambio de posición entre tiempo). Pero ahora es interesante continuar con la propuesta de Newton: hacer que “?” sea infinitesimalmente pequeña. Esto tiene dos implicaciones; la primera es que, al acercarse así, f(x + ?) y f(x), la recta cortará a la curva sólo en punto y se convertirá en una tangente (por definición) a la curva. La segunda implicación es que, al acercarse el tiempo dado por (x + ?) y (x) en la misma condición, se tendrá ahora un instante. De esta forma, la propuesta de Newton plantea que su aproximación en el límite será la velocidad del móvil en un instante, esto es, velocidad instantánea. Dicho de otra forma, será posible describir el comportamiento del punto en movimiento punto a punto, instante a instante.

Resulta sorprendente el planteamiento obtenido, ya que es una herramienta de análisis que no se había logrado por otro medio. Al aplicar de manera conjunta los conceptos de función y límite, se llega a este nuevo concepto que matemáticamente se denomina derivada de una función, una nueva herramienta que acepta interpretaciones equivalentes para una variedad muy amplia de problemas y, a partir de la función que define el fenómeno, permite determinar la velocidad máxima a que un auto puede circular en una carretera, la concentración de una mezcla o las variaciones en la bolsa, esto es, un sinfín de posibilidades.