G, el diminuto número sin el que la vida no existiría

Es un número que Newton descubrió, Cavendish valoró y Einstein entendió

6,67 x 10-¹¹ o 0,000000000067 es un número diminuto pero sin él, la vida, el Universo y todo simplemente no existiría.

Eso es porque ese número dicta la fuerza de gravedad, esa atracción constante que toda materia ejerce sobre el resto de materia, que

es sorprendentemente ubicua pero también increíblemente débil.

Su potencia se cuantifica con la llamada constante gravitacional, un número conocido sencillamente como G.

Y si quieres experimentar su debilidad sólo tienes que levantar los brazos horizontalmente.

Su debilidad se evidencia con acciones tan comunes como ésta.

Toda la fuerza de la masa de la Tierra hala tus brazos hacia abajo. No obstante, no te cuesta mucho esfuerzo vencerla.

Sin palabras

Fue debido a su extremada pequeñez que, tras descubrir la Ley de Gravitación Universal, Isaac Newton incluyó G en su ecuación pero

no lo pudo calcular.

Pero un siglo más tarde, un inglés llamado Henry Cavendish se planteó el reto de determinar el valor de G y, por ende, la fuerza de la gravedad.

Cavendish era un hombre adinerado del Londres del siglo XVIII, un poco excéntrico y quizás triste, pues no tenía muchos amigos.

No hablaba casi con nadie, ni siquiera con las doncellas que trabajaban en su casa, pues su timidez le impedía hablar con mujeres. Les

tenía que dejar mensajes en la mesa del hall para comunicarles cosas como qué le apetecía almorzar.

Así que dedicó toda su vida a la ciencia, sin que ningún otro interés lo distrajera.

Henry Cavendish además mostró que los gases se podrían pesar, que el aire es una mezcla y que el agua no es un elemento. En física,

mostró que la densidad de la Tierra era 5,5 veces mayor que la del agua. Gran parte de su física fue inédita hasta que James Clerk

Maxwell lo publicó en la década de 1870, y por lo tanto no fue tan influyente como podría haber sido.

Para encontrar el valor exacto de G, construyó un aparato.

"El aparato es muy simple. Consiste de un brazo de madera de 6 pies de longitud hecho de manera que sea fuerte pero liviano. El brazo

está suspendido en posición horizontal con un delgado cable de seda de 40 pulgadas, y de cada extremo cuelga una esfera de plomo de

unas dos pulgadas de diámetro.

"Todo está encerrado en una caja de madera, para defenderlo del viento".

Cerca de las dos bolas que Cavendish menciona, puso otras dos esferas estacionarias, para que hubiera una atracción que retorciera el

aparato y la fibra de seda. Añadió un espejo de manera que el movimiento se reflejara en la pared, para verlo mejor.

Esa desviación era proporcional a la fuerza de la atracción gravitacional entre las bolas grandes estacionarias y las pequeñas.

El problema es que estas últimas se podían mover con cualquier vibración, algo que Cavendish tuvo en cuenta

Modelo del aparato de Cavendish.

"Resuelto a prevenir errores, decidí poner el aparato en una habitación que permaneciera constantemente cerrada y observarlo desde afuera con un telescopio".

Con todo ese cuidado, encontró la respuesta... ese diminuto número con el que empezamos:

G = 6,67 x 10-¹¹ Nm²/kg²

Al verlo escrito así, a quienes no somos expertos, ya no nos parece tan sencillo, así que le preguntamos al astrofísico y escritor de ciencia Marcus Chown cómo se define G.

"Su definición exacta es la fuerza gravitacional entre dos masas de 2 kilogramos que están a un metro de distancia".

"Como es una fuerza tan fantásticamente pequeña sólo tiene un efecto apreciable a escala planetaria: cuando la masa es grande".

Con sólo la fuerza de G, a un corredor de 100 metros le tomaría un año llegar a la meta

Un misterioso bamboleo

Por años, los científicos pensaron que el enigma de la gravedad estaba resuelto: Newton encontró la ecuación y Cavendish el valor de la G que aparecía en ella.

La fórmula parecía predecir todos los fenómenos terrestres y celestiales.

Pero en la década de 1850s los astrónomos notaron un misterioso bamboleo en la órbita del planeta Mercurio.

• Vulcano, el planeta fantasma buscado por más de medio siglo

Pero en 1915, en la Academia Prusiana de las Ciencias finalmente se publicó la solución a ese particular rompecabezas... y varios otros: no sólo la teoría de Newton estaba errada sino que había que cambiar fundamentalmente la idea que se tenía de la realidad.

El responsable de este desbarajuste de la visión que se tenía del Universo fue Albert Einstein quien, basado en su Teoría de la Relatividad General, había comprendido que si el espacio-tiempo es curvo, cuando las cosas caen en un campo gravitacional, siguen las curvas naturales del espacio.

No obstante, no todo era nuevo en la flamante fórmula de la gravedad pues seguía dependiendo del diminuto G.

• Einstein estaba en lo cierto: el "monstruo gravitatorio" que permitió comprobar la teoría de la relatividad en condiciones extremas
• 
• Einstein se quedó con la G

La teoría de Einstein con la medición de Cavendish parecen poder describir con precisión cómo cada trozo del Universo atrae a todos los otros trozos del Universo, desde las fuerzas que hacen que una estrella colapse, hasta las que mantienen galaxias enteras juntas.

Y todo esto, ¿afecta tu vida?

Muchísimo más que 0,000000000067.

Si su valor fuera diferente, nada sería igual. De hecho, muy probablemente no existiríamos.

Si la constante gravitacional hubiera sido 2% más alta, la fuerza de gravedad sería más potente, lo que significaría que la materia en el centro del Sol estaría comprimida, y cuando las cosas se comprimen la temperatura aumenta.

El Sol habría quemado todo su combustible en mucho menos de 2.000 millones de años. Y, dado que los organismos multicelulares tomaron 3.000 millones de años en aparecer, eso significa que no habría habido vida.

No sólo estamos hechos de polvo de estrellas; sin ellas, no existiríamos.

Un Universo sin estrellas para iluminar y calentar los planetas ni para producir con sus reacciones termonucleares mucho carbono, hidrógeno y oxígeno, sería un espacio negro con astros muertos.

Así que si G hubiera sido más fuerte, las estrellas se habrían quemado demasiado pronto, y la vida no habría tenido la oportunidad de evolucionar.

Si hubiera sido más débil, la situación habría sido igualmente lúgubre pues las estrellas ni siquiera se habrían podido formar: no habría soles.

Por suerte, G no es demasiado fuerte o demasiado débil: está perfectamente sintonizado para la vida.

Ahora hablemos de Florence:

Florence Nightingale la Estadística Británica

El 12 de Mayo se celebra el Día Internacional de la Enfermería en honor al natalicio de la que se considera la fundadora de la enfermería moderna, Florence Nightingale.

Esta mujer de clase acomodada nació en Florencia, pero finalmente se radicó en Inglaterra. Fue educada en casa en parte importante por su padre, un graduado de Cambridge, y siempre se destacó en Ciencias y en particular en Matemáticas. Su deseo fue estudiar matemáticas, lo que fue resistido por sus padres porque era mujer y era el año 1840. Finalmente su férrea determinación dio frutos y fue discípula privada del matemático James Joseph Sylvester, un destacado matemático fundador del American Journal of Mathematics en su estadía por los EE.UU. y al que se le atribuye dar a varios objetos matemáticos sus nombres actuales como  “grafo”, “matriz” y “discriminante”.

Esta mujer excepcional tenía además una vocación religiosa tan intensa como su pasión por la ciencia que la llevó a sentir que Dios le había encomendado una misión. En su diario se lee “Dios ha hablado conmigo y me ha llamado a su servicio. Que forma ha de tomar dicho servicio es algo que la Voz no mencionó”. A los 24 años decidió cuál era su camino y acudió a Salisbury a formarse como enfermera. Sus padres se opusieron rotundamente a que su hija siguiera una profesión destinada a los pobres y los sirvientes y lucharon con ella por 10 años hasta que finalmente comprendieron que casar a su hija con un candidato acorde a su posición era una quimera. Finalmente viajó a Alemania a formarse como enfermera  y gracias a su formación científica en agosto de 1853 Florence fue nombrada superintendente del hospital para mujeres en Harley Street.

Su invaluable aporte como enfermera de campo durante la guerra de Crimea la convirtió en una heroína. Las crónicas dicen que fue la primera vez que las tropas regulares fueron tratadas con decencia y respeto.

Tras su regreso de la guerra, Florence Nightingale utilizó su fama para denunciar las deficientes condiciones de los hospitales. Esto llegó a oídos de la Reina Victoria y por su orden se formó un equipo con Florence y los matemáticos William Farr y John Sutherland que analizaron los datos recogidos durante la guerra. El estudio mostró una realidad devastadora: 16,000 de las 18,000 muertes durante la guerra fueron por enfermedades derivadas de las insalubres condiciones de los hospitales.

GRÁFICAS DE FLORENCE

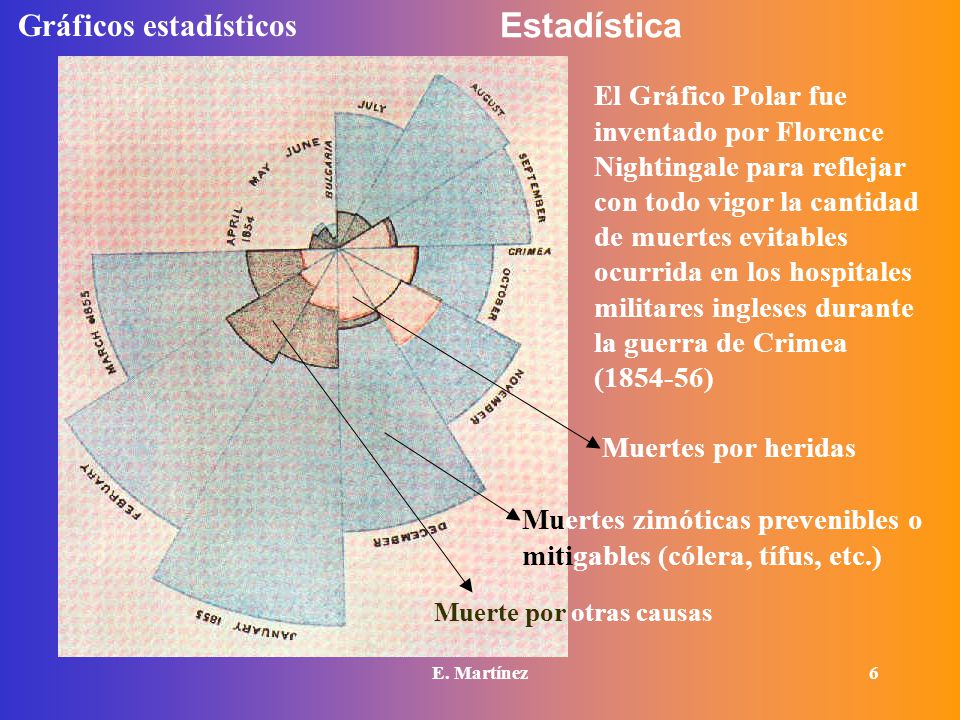
↑ 1858 – LA MORTALIDAD DEL EJÉRCITO BRITÁNICO

Llegando a  la conclusión de que era la manera mas efectiva de de convertir datos en información, Nightingale, 

comenzó a implementar gráficos estadísticos en sus informes que entregaba al parlamento británico. En la parte

superior se puede apreciar algunos de sus diagramas claves, sobre la mortalidad del ejército británico, publicado en

1858. El gráfico circular, cuyo primer desarrollo se debió a William Playfair en 1801, es conocido como diagrama de área

polar o como diagrama de la rosa de Nightingale. El círculo de la derecha tiene 12 sectores que representan los

primeros 12 meses de la guerra. El círculo de la izquierda representan los 12 meses consiguientes. Las formas

superpuestas  muestran las tasas de mortalidad mensual y cómo la Comisión Sanitaria, que se envió en medio de la

guerra, redujo drásticamente la tasa de mortalidad.