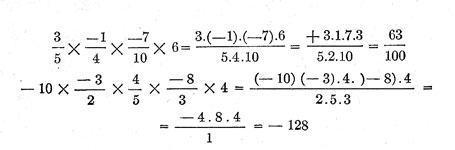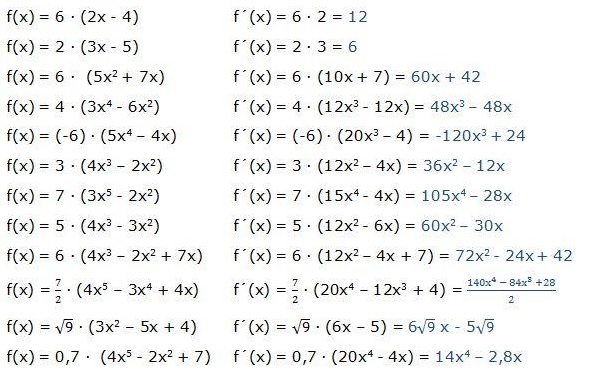Aplicaciones de la derivada en la vida real

Como ya hemos visto en entradas anteriores, las matemáticas permiten crear modelos teóricos que sirven para explicar fenómenos de la vida real. 

Ya sabemos que la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función según cambie el valor de su variable independiente o, dicho de otro modo, la derivada de una función nos indica el ritmo con el que dicha función varía (crece, decrece o permanece constante) cuando se producen pequeños cambios en la variable independiente.

Fíjate, no es lo mismo...

En los tres casos descendemos, pero no al mismo ritmo. En el primer caso, descendemos despacio; en el segundo, el descenso es más rápido pero en el tercero, ¡es una locura!

Mediante el estudio de funciones y, más concretamente, mediante el uso de la derivada podemos conocer:

• la variación del espacio en función del tiempo
• el crecimiento de una bacteria en función del tiempo
• el desgaste de un neumático en función del tiempo
• el beneficio de una empresa en función del tiempo... 

De ahí que el uso de la derivada resulte fundamental en muchas situaciones de la vida cotidiana. 

En matemáticas utilizamos derivadas para estudiar el comportamiento de las funciones, hallar los intervalos de crecimiento, de decrecimiento, los máximos y mínimos relativos y absolutos, los intervalos de concavidad y convexidad, los puntos de inflexión...

También nos ayudamos de las derivadas para resolver problemas de optimización (conseguir el valor óptimo de una función sujeta o no a ciertas condiciones)

Si estás interesado en profundizar en estas aplicaciones puedes hacerlo en los siguientes enlaces:

 

Aplicaciones de las derivadas: Estudio de la gráfica de una función

Aplicaciones de las derivadas: Problemas de optimización

Pero las aplicaciones de las derivadas no se reducen al ámbito matemático. Vamos a concretar algunas de las aplicaciones del concepto de derivada a diversos campos de la vida real.

APLICACIONES A LA GEOMETRÍA

• La derivada de la superficie o área es la longitud.

• La derivada del volumen es la superficie.

APLICACIONES A LA FÍSICA

CINEMÁTICA

• La velocidad instantánea es la derivada del espacio respecto del tiempo.

• La aceleración instantánea es la derivada de la velocidad respecto del tiempo. Por tanto, la aceleración instantánea es la segunda derivada del espacio respecto del tiempo.

DINÁMICA

• La derivada del momento lineal con el tiempo es la fuerza.

• La derivada de la fuerza con respecto a la posición es la energía (potencial, cinética, trabajo...)

TERMODINÁMICA

• Si una sustancia dada se mantiene a una temperatura constante, entonces su volumen V depende de la presión P. La compresibilidad isotérmica está relacionada con la derivada del volumen respecto a la presión mediante la siguiente fórmula:

FÍSICA DE MATERIALES

• La derivada de la masa con respecto a la longitud/superficie/volumen es la densidad.

ELECTROSTÁTICA

• La derivada de la carga eléctrica con respecto al tiempo es la intensidad de corriente.

APLICACIONES A LA QUÍMICA

• Cuando se produce una reacción química, las concentraciones de los reactivos y productos van cambiando con el tiempo hasta que se produce el equilibrio químico, en el cual las concentraciones de todas las sustancias permanecen constantes. La velocidad de reacción química es la derivada de la concentración de un reactivo o producto en función del tiempo.

APLICACIONES A LA BIOLOGÍA

• Permite el estudio de evolución de poblaciones de bacterias, de otras especies animales, de plantas... Se han deducido expresiones para el "Número de individuos" (tamaño de la población) según el tipo de crecimiento que presentan, y para obtener dicho crecimiento se necesitan las derivadas:

• Se sabe que un material radioactivo se desintegra con una rapidez proporcional a la cantidad presente en cualquier instante, por lo que, usando el cálculo diferencial, se puede encontrar la expresión de la cantidad de material radiactivo en función del tiempo.

APLICACIONES A LA MEDICINA

• El concepto de derivada permite conocer la evolución de ciertas enfermedades puesto que podemos modelizar el número de bacterias, virus, células infectadas... y estudiar su ritmo de crecimiento/decrecimiento al utilizar fármacos, comprobando así su efectividad.

• Podemos estudiar la evolución de ciertas epidemias puesto que podemos modelizar el número de enfermos en función del tiempo transcurrido.

APLICACIONES A LA INGENIERÍA

• Los ingenieros químicos o ingenieros en procesos utilizan la derivada para representar fenómenos que ocurren en un proceso mediante el uso de ecuaciones diferenciales.

• Se utilizan en los sistemas de tratamiento de aguas residuales así como en la recogida y tratamiento de residuos.

• También son de gran utilidad en los estudios de contaminación y diagnóstico.

• En ingeniería industrial se utiliza mucho la derivada para reducir costes al fabricar un producto (optimización).

APLICACIONES A LA ARQUITECTURA

• En arquitectura, es frecuente trabajar con curvas complejas (paraboliodes, hiperboloides, superficies irregulares...) de las que necesitamos obtener información relevante (máximos, mínimos, zonas de concavidad y convexidad...)

• También se utiliza la derivada (y la integral) para calcular áreas y volúmenes de regiones y sólidos de revolución.

• Para resolver problemas de optimización (reducir costes de los materiales)

• Resultan de gran utilidad en el diseño de vías y carreteras, más específicamente, en el estudio de su curvatura.

APLICACIONES A LA ECONOMÍA

• El uso de la derivada permite resolver múltiples problemas de optimización en el ámbito económico (conseguir que una empresa obtenga el máximo beneficio, los ingresos máximos, los costes mínimos...)

• También permite estudiar la evolución de determinados fenómenos de índole económica (índice de la bolsa, evolución de la economía, beneficios de una empresa...) en función del tiempo (crecimiento, decrecimiento, máximos y mínimos...), proporcionando información muy útil para el empresario a la hora de tomar decisiones.

• La derivada es una herramienta de gran utilidad en economía puesto que nos permite realizar cálculos marginales, es decir, hallar la razón de cambio cuando se agrega una unidad adicional al total, sea cual sea la cantidad económica que se esté estudiando (coste, ingreso, beneficio, producción...)

- - - - - - - -

Sin duda, hemos dejado por mencionar muchas otras aplicaciones de la derivada pero considero que, después de las que hemos indicado, te habrás hecho una idea de la gran importancia que tiene esta herramienta tanto en el ámbito científico como social.

Espero que todo esto te motive para afrontar el estudio de las derivadas con ilusión puesto que, como has podido comprobar, es muy probable que en el futuro tengas que utilizar con frecuencia esta herramienta.