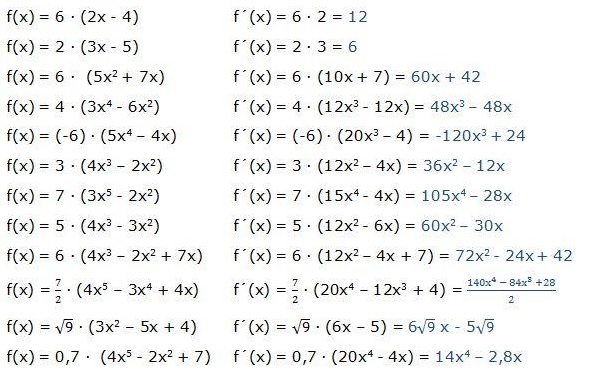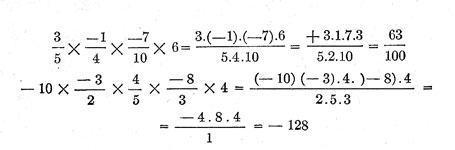La Derivada, sus aplicaciones en la vida real

1. Muchas veces, con la ayuda del sentido común, estamos derivando sin darnos apenas cuenta. Naturalmente, uno no necesita derivar en la vida diaria fuera del trabajo (y tampoco en la mayor parte de las actividades profesionales). Sin embargo, las derivadas son necesarias en muchas aplicaciones prácticas en biología, mecánica, en medicina bacteriológica, etc. Especialmente el concepto de derivada es fundamental para comprender y derivar fórmulas que luego tienen una aplicación importante en la industria y en la ciencia en general, que es la que definitivamente inspira las innovaciones industriales. Las derivadas se utilizan para optimizar sistemas que se expresan mediante funciones más o menos complejas. Otra de sus aplicaciones es hallar los valores máximos o mínimos de ciertas expresiones (por ejemplo, una inversión compleja en economía financiera). Otra es hallar los intervalos de crecimiento o decrecimiento de valores de interés, siempre que se puedan representar mediante funciones. Si sabemos por ejemplo que los campeones de 100 metros lisos corren en esa distancia en unos 10 segundos, al calcular la velocidad promedio de 10 metros por segundo (36km por hora) estamos haciendo una derivada, bajo el supuesto de que la velocidad fuera constante (velocidad promedio). El ejemplo clásico se da en la cinemática, en donde la derivada se aplica para saber la velocidad y aceleración de un móvil. Por ejemplo, si un auto se desplaza a una cierta distancia

2. En un cierto tiempo, eso tiene una fórmula para calcular la posición con respecto al tiempo. Si queremos saber la velocidad, entonces derivamos una vez esa fórmula, y para saber la aceleración hacemos la segunda derivada, de ahí viene el hecho de que la derivada sea una velocidad) Otro ejemplo más complejo seria nombrar la mecánica de fluidos, lo que hizo posible la creación de las presas o los aviones. También esta el electromagnetismo, lo que hizo posible la creación de los electrodomésticos que usamos todos los días (TV, neveras, microondas, entre otros) Como se ve la derivada tiene muchas aplicaciones en la física, esto puede ser debido a que el creador del cálculo diferencial es el mismo que invento la física (Isaac Newton).
3. 3. Las derivadas representan razones de cambio en su aspecto más simple; así pues, cada vez que prendes tu teléfono celular, cuando vez que un edificio resiste el embate del viento, la aguja que se mueve en el velocímetro del automóvil, todo eso son las derivadas funcionando. En ingeniería te sirven para calcular, por ejemplo: Como varía la temperatura en un tubo cuando aumenta la presión (refrigeradores) Cuánta fuerza necesitas para revolver una mezcla a velocidad constante en función de como varía su densidad al aumentar los ingredientes (una fábrica de mantequilla de maní) Cuánto tiempo le durará la pila a tu celular en función del cambio de consumo de corriente durante una llamada. El caso de la física es muy similar al de la ingeniería (ingeniería es como física aplicada) pero a nivel un poco más teórico; por ejemplo. La variación de la aceleración en función a la pérdida de masa y empuje en el despegue de un cohete espacial La variación de la cantidad de radiación del carbono14 en función del tiempo cuando mides la edad de los fósiles Los corrimientos en frecuencia de la luz que llega de las estrellas en función de la distancia para ayudar a conocer su edad y/o distancia. Por su parte administración es mucho menos notable. La administración se basa a veces en la estadística o en los datos contables para dirigir el curso de las acciones empresariales en base a los datos del pasado; por ejemplo. En función a la demanda de los años anteriores de un juguete y del crecimiento poblacional y varianza del poder adquisitivo en el año, determinar la producción de cada juguete. En función a la cantidad de personal existente, rendimientos e ingresos, determinar la cantidad de posible personal a contratar, para que éste sea sustentable
4. En un cierto tiempo, eso tiene una fórmula para calcular la posición con respecto al tiempo. Si queremos saber la velocidad, entonces derivamos una vez esa fórmula, y para saber la aceleración hacemos la segunda derivada, de ahí viene el hecho de que la derivada sea una velocidad) Otro ejemplo más complejo seria nombrar la mecánica de fluidos, lo que hizo posible la creación de las presas o los aviones. También esta el electromagnetismo, lo que hizo posible la creación de los electrodomésticos que usamos todos los días (TV, neveras, microondas, entre otros) Como se ve la derivada tiene muchas aplicaciones en la física, esto puede ser debido a que el creador del cálculo diferencial es el mismo que invento la física (Isaac Newton).
5. 3. Las derivadas representan razones de cambio en su aspecto más simple; así pues, cada vez que prendes tu teléfono celular, cuando vez que un edificio resiste el embate del viento, la aguja que se mueve en el velocímetro del automóvil, todo eso son las derivadas funcionando. En ingeniería te sirven para calcular, por ejemplo: Como varía la temperatura en un tubo cuando aumenta la presión (refrigeradores) Cuánta fuerza necesitas para revolver una mezcla a velocidad constante en función de como varía su densidad al aumentar los ingredientes (una fábrica de mantequilla de maní) Cuánto tiempo le durará la pila a tu celular en función del cambio de consumo de corriente durante una llamada. El caso de la física es muy similar al de la ingeniería (ingeniería es como física aplicada) pero a nivel un poco más teórico; por ejemplo. La variación de la aceleración en función a la pérdida de masa y empuje en el despegue de un cohete espacial La variación de la cantidad de radiación del carbono14 en función del tiempo cuando mides la edad de los fósiles Los corrimientos en frecuencia de la luz que llega de las estrellas en función de la distancia para ayudar a conocer su edad y/o distancia. Por su parte administración es mucho menos notable. La administración se basa a veces en la estadística o en los datos contables para dirigir el curso de las acciones empresariales en base a los datos del pasado; por ejemplo. En función a la demanda de los años anteriores de un juguete y del crecimiento poblacional y varianza del poder adquisitivo en el año, determinar la producción de cada juguete. En función a la cantidad de personal existente, rendimientos e ingresos, determinar la cantidad de posible personal a contratar, para que éste sea sustentable.

           https://es.slideshare.net/josefaria039gmailcom/la-derivada-sus-aplicaciones-en-la-vida-real