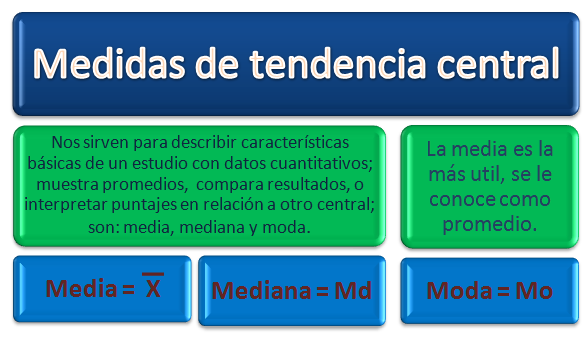
Principales características de las medidas de tendencia central
Se presenta un cuadro donde se diferencia la Media, la Mediana y la Moda.
|
Principales características de las medidas de tendencia central |
||
|
Media |
Mediana |
Moda |
|
Conocida como promedio, se calcula con la suma de los datos y se divide por la cantidad de datos que tenga el ejercicio a resolver. Para datos pequeños se sigue la siguiente fórmula:
X son los datos n los números de datos de la muestra
Cuando son grandes (datos agrupados) la fórmula se transforma en:
La media es sensible a la presencia de datos extremos. Ejemplo 1 La media aritmética de los números 8,3,5,12,10 es:
Ejemplo 2 Si 5,8,6 y 2 ocurren con frecuencia 3,2,4 y 1 en este orden la media aritmética es:
|
Conjunto de datos ordenados de menor a mayor, en donde la mediana corresponde al dato central. Se debe tener en consideración si la cantidad de datos es par o impar, con el fin de aplicar lo siguiente:
para su cálculo. En datos agrupados, la mediana se puede estimar como:
Donde: Li = Es el límite inferior del intervalo de la clase que contiene a la mediana A = amplitud del intervalo n = tamaño de la muestra. Ni-1 = frecuencia acumulada del intervalo anterior.
La mediana es muy útil cunado la distribución de la variable es poco simétrica.
Ejemplo 1 La mediana de los números 8,3,5,12,10 es: 3,5,8,10,12 (5+1) / 2 = 3(lugar) por lo tanto, la mediana es 8.
Ejemplo 2 una distribución de frecuencia de madres que asisten a un programa de lactancia materna, clasificadas según el número de partos. Por tratarse de una variable en escala discreta, las clases o categorías asumen sólo ciertos valores: 1, 2, 3, 4, 5.
Yi= n° de partos ni = frecuencia absoluta yi*ni = n° de partos * frecuencia Ni= frecuencia acumulada.
Como la mediana es el valor de la variable que corresponda a la frecuencia acumulada que supere inmediatamente a n/2. En los datos de la tabla, Me es igual a 3, ya que 42/2 es igual a 21 (media) y la frecuencia acumulada que supera inmediatamente a 21 es 33, que corresponde a un Yi igual a 3. |
Es aquel valor observado que tiene mayor frecuencia. En datos agrupados se puede considerar como moda a la marca de clase de la categoría con mayor frecuencia. Cuando dos valores ocurren con la misma frecuencia y ésta es la más alta, ambos valores son modas, siendo bimodal. Puede llegar a ser trimodal o mayor (polimodal). Cuando ningún valor se repite se dice que no hay moda. En un polígono de frecuencia la moda corresponde al valor de la variable que está bajo el punto más alto del gráfico. Una muestra puede tener más de una moda.
Ejemplo 1 El Cruz Azul en sus últimos 10 partidos a metido los siguientes números de goles: 2,1,0,3,4,5,4,3,1 y 1 La moda es 1
Utilizando el ejemplo de los partos (ejemplo 2 expuesto en la mediana). En los datos de la tabla el valor de la moda es 3 ya que este valor de variable corresponde a la mayor frecuencia absoluta =16. |
Bibliografía
Boils, G. (Septeimbre de 2002). Biblioteca CF+S. Obtenido de El Banco Mundial y la política de vivienda en México: http://habitat.aq.upm.es/boletin/n29/agboi.html
BOILS, G. (2004). El Banco Mundial y la política de vivienda en México. Rev. Mex. Sociol, 66. Obtenido de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0188-25032004000200004
IDB. (s.f.). IDB Impreving lives. Obtenido de https://indesvirtual.iadb.org/mod/page/view.php?id=66844&lang=es
Ischinger, B. (19 de Octubre de 2010). OECD. Obtenido de Implementación de Política Educativa: México: https://www.oecd.org/centrodemexico/medios/implementaciondepoliticaeducativamexico.htm
Maldonado, A. (2000). Los organismos internacionales y la educación en México: El caso de la educación superior y el Banco Mundial. Perfiles educativos, 22(87), 51-75. Obtenido de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0185-26982000000100004
Quevedo, F. (Marzo de 2011). Medidas de tendencia central y dispersión. Medwave. doi:10.5867
UNAM. (1 de Abril de 2016). Blogs de la FES Acatlán. Obtenido de http://blogs.acatlan.unam.mx/calidad/files/2016/04/1.-Medidas-de-tendencia-central.pdf
UNESCO. (22 de Diciembre de 2015). PLAN DE TRABAJO. Obtenido de http://www.lacult.unesco.org/docc/20151222_Plan_Trabajo_ESP.pdf
Temas relacionados:
#media #mediana #moda
Esta web se reserva el derecho de suprimir, por cualquier razón y sin previo aviso, cualquier contenido generado en los espacios de participación en caso de que los mensajes incluyan insultos, mensajes racistas, sexistas... Tampoco se permitirán los ataques personales ni los comentarios que insistan en boicotear la labor informativa de la web, ni todos aquellos mensajes no relacionados con la noticia que se esté comentando. De no respetarse estas mínimas normas de participación este medio se verá obligado a prescindir de este foro, lamentándolo sinceramente por todos cuantos intervienen y hacen en todo momento un uso absolutamente cívico y respetuoso de la libertad de expresión.
No hay opiniones. Sé el primero en escribir.







 = 7.6
= 7.6